This New Decomposition Framework Makes Multi-Agent Pathfinding More Scalable

:::info
Authors:

1. Zhuo Yao
2. Wei Wang

:::

Table Of Links

ABSTRACT

I. INTRODUCTION

II. RELATED WORKS

III. PRELIMINARIES

IV. METHODOLOGY

V. RESULTS OF DECOMPOSITION

VI. RESULTS OF DECOMPOSITION’S APPLICATION

VII. CONCLUSION, ACKNOWLEDGMENTS AND REFERENCES

ABSTRACT

Generally, the calculation and memory space required for multi-agent path finding (MAPF) grows exponentially as the number of agents increases. This often results in some MAPF instances being unsolvable under limited computational resources and memory space, thereby limiting the application of MAPF in complex scenarios. Hence, we propose a decomposition approach for MAPF instances, which breaks down instances involving a large number of agents into multiple isolated subproblems involving fewer agents.

Moreover, we present a framework to enable general MAPF algorithms to solve each subproblem independently and merge their solutions into one conflict-free final solution, without compromising on solvability. Unlike existing works that propose isolated methods aimed at reducing the time cost of MAPF, our method is applicable to all MAPF methods. In our results,

we apply decomposition to multiple stateof-the-art MAPF methods using a classic MAPF benchmark1 . The decomposition of MAPF instances is completed on average within 1s, and its application to seven MAPF methods reduces the memory usage and time cost significantly, particularly for serial methods. To facilitate further research within the community, we have made the source code of the proposed algorithm publicly available.

I. INTRODUCTION

Multi-agent pathfinding (MAPF), as its name suggests, computes a set of collision-free paths for multiple agents from their respective starting locations to target locations. Existing methods for MAPF are capable of determining optimal or bounded suboptimal solutions, but efficiency remains a key factor limiting its application. Researchers have proposed novel methods to address this issue, such as trading off solution quality to reduce runtime, reducing search branch factors, and solving agents independently based on their priorities.

However, these techniques are often not applicable to all MAPF methods, as they are limited to specific types of MAPF problems. Motivated by the phenomenon that the cost of solving MAPF instances grows exponentially as the number of agents increases [7], we propose a novel approach to reduce the cost of MAPF methods by decomposing a MAPF instance into multiple smaller subproblems. These subproblems are solved independently, while considering the solutions of other subproblems as dynamic obstacles.

This idea bears resemblance to Priority-Based Search (PBS) [11], which assigns a unique priority to each agent and solves agents separately in decreasing priority order. PBS can be viewed as decomposing a MAPF instance into subproblems,

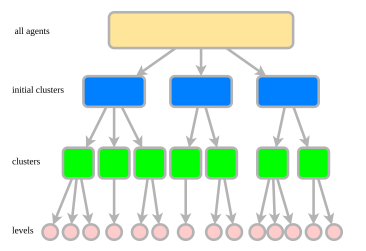
each involving only one agent. While PBS is efficient, it lacks a guarantee of completeness. In contrast, our approach aims to decompose MAPF instances without compromising their solvability. We formulate the decomposition of MAPF instances as a progressive optimization problem. Initially, we decompose the MAPF instance into multiple subproblems without restricting the order of solving, and then further split them into smaller subproblems with a limited solving order.

To ensure solvability and minimize the size of each decomposition, we evaluate the solvability of each step of decomposition, allowing only those decompositions that do not compromise solvability. As a result, we demonstrate the performance of our method across various maps and illustrate its improvement on multiple cutting-edge MAPF methods. The contributions of this manuscript are listed as follows:

1. We introduce a novel problem of decomposing a MAPF instance into solvable subproblems to reduce the solving cost. Additionally, we propose a novel method that decomposes a MAPF instance into multiple subproblems without compromising solvability. An overview of our method is depicted in Fig. 1.

2. We present a framework that enables general MAPF methods to solve subproblems independently and merge their solutions to obtain the solution of the original problem.

3. We conduct extensive testing to evaluate how the decomposition of MAPF instances influences various MAPF methods using classic MAPF datasets. We evaluate the impact in terms of time cost, memory usage, success rate, and solution quality. The remainder of this article is organized as follows. In Section II, we review related problems and methods aimed at reducing the solving cost of MAPF instances. We then define basic terminology in Section III and introduce our method in Section IV. Our test results regarding the performance of decomposition under various maps are presented in Section V, followed by an examination of how decomposition benefits multiple cutting-edge MAPF methods in Section VI. Finally, Section VII concludes this article.

:::info
This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::