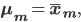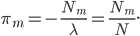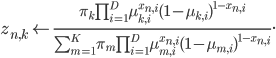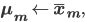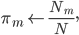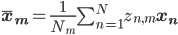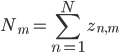Expectation-Maximization Algorithm for Bernoulli Mixture Models (Tutorial)
Even though the title is quite a mouthful, this post is about two really cool ideas:
- A solution to the “chicken-and-egg” problem (known as the Expectation-Maximization method, described by A. Dempster, N. Laird and D. Rubin in 1977), and
- An application of this solution to automatic image clustering by similarity, using Bernoulli Mixture Models.
For the curious, an implementation of the automatic image clustering is shown in the video below. The source code (C#, Windows x86/x64) is also available for download!
Automatic clustering of handwritten digits from MNIST database using Expectation-Maximization algorithm
While automatic image clustering nicely illustrates the E-M algorithm, E-M has been successfully applied in a number of other areas: I have seen it being used for word alignment in automated machine translation, valuation of derivatives in financial models, and gene expression clustering/motif finding in bioinformatics.
As a side note, the notation used in this tutorial closely matches the one used in Christopher M. Bishop’s “Pattern Recognition and Machine Learning”. This should hopefully encourage you to check out his great book for a broader understanding of E-M, mixture models or machine learning in general.
Alright, let’s dive in!
1. Expectation-Maximization Algorithm
Imagine the following situation. You observe some data set 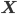
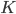
Let 
Clearly, if you knew 

Here’s a general idea of how E-M algorithm tackles it. First of all, all images are assigned to clusters arbitrarily. Then we use this assignment to modify the parameters of the clusters (e.g. we change what object is represented by that cluster) to maximize the clusters’ ability to explain the data; after which we re-assign all images to the expected most-likely clusters. Wash, rinse, repeat, until the assignment explains the data well-enough (i.e. images from the same clusters are similar enough).
(Notice the words in bold in the previous paragraph: this is where the expectation and maximization stages in the E-M algorithm come from.)
To formalize (and generalize) this a bit further, say that you have a set of model parameters 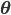
To solve the problem of cluster assignments we effectively need to find model parameters 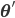
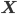
Using some simple algebra we can show that for any latent variable distribution 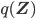
begin{align}
ln ,text{Pr}(mathbf{X} | theta) = mathcal{L}(q, theta) + text{KL}(q || p), label{eq:logLikelihoodDecomp}
end{align}
where 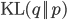
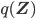
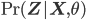
begin{align}
mathcal{L}(q, theta) := sum_{mathbf{Z}} q(mathbf{Z}) left( mathcal{L}(theta) – ln q(mathbf{Z}) right)
end{align}
with 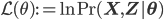
To understand what the E-M algorithm does in the expectation (E) step, observe that 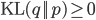
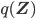
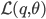
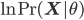
Then, in the E step, the gap between the 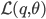
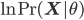
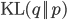
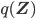
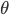
Since 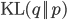
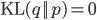
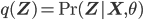
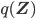
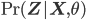
To maximize the model parameters in the M step, the lower bound 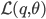
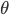
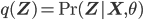
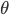
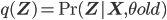
The function 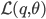
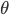
begin{align*}
theta^text{new} &= underset{mathbf{theta}}{text{arg max }} left. mathcal{L}(q, theta) right|_{q(mathbf{Z}) = ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old})} \
&= underset{mathbf{theta}}{text{arg max }} left. sum_{mathbf{Z}} q(mathbf{Z}) left( mathcal{L}(theta) – ln q(mathbf{Z}) right) right|_{q(mathbf{Z}) = ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old})} \
&= underset{mathbf{theta}}{text{arg max }} sum_{mathbf{Z}} ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old}) left( mathcal{L}(theta) – ln ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old}) right) \
&= underset{mathbf{theta}}{text{arg max }} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right] – sum_{mathbf{Z}} ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old}) ln ,text{Pr}(mathbf{Z} | mathbf{X}, theta^text{old}) \
&= underset{mathbf{theta}}{text{arg max }} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right] – (C in mathbb{R}) \
&= underset{mathbf{theta}}{text{arg max }} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right],
end{align*}
i.e. in the M step the expectation of the joint log likelihood of the complete data is maximized with respect to the parameters 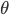
So, just to summarize,
- Expectation step:
- Maximization step:
(where superscript
indicates the value of parameter
at time
).
Phew. Let’s go to the image clustering example, and see how all of this actually works.
2. Bernoulli Mixture Models for Image Clustering
First of all, let’s represent the image clustering problem in a more formal way.
2.1. Formal description
Say that we are given 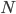
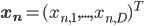
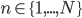
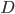
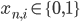
Assuming that the pixels are conditionally independent from each other (i.e. that 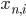
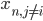
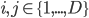
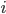
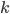
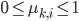
To incorporate some prior knowledge about the image assignment to 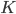
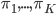
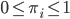
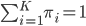
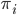
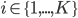
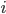
Let say that the model parameters include the pixel distributions of each cluster and the prior knowledge about the image assignments, i.e. 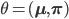

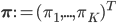
Then, the likelihood of a single training image 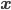
begin{align}
,text{Pr}(mathbf{x} | theta) = ,text{Pr}(mathbf{x} | mathbf{mu}, mathbf{pi}) = sum_{k = 1}^K pi_k ,text{Pr}(mathbf{x}|mathbf{mu_k})
end{align}
where the probability that 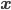
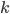
begin{align}
,text{Pr}(mathbf{x}|mathbf{mu_k}) = prod_{i = 1}^D mu_{k, i}^{x_i} (1 – mu_{k, i})^{1 – x_i}.
end{align}
To model the assignment of images to clusters, associate a latent 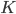
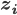
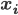
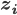
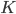
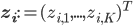
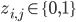
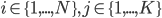
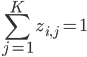
Furthermore, let the marginal distribution over 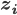

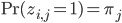
begin{align}
,text{Pr}(mathbf{z_n} | mathbf{pi}) = prod_{i = 1}^K pi_i^{z_{n, i}}.
end{align}
Similarly, let 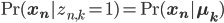
begin{align}
,text{Pr}(mathbf{x_n} | mathbf{z_n}, mathbf{mu}, mathbf{pi}) = prod_{k = 1}^K ,text{Pr}(mathbf{x_n} | mathbf{mu_k})^{z_{n, k}}.
end{align}
By combining all latent variables 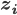
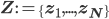
begin{equation} label{eq:probZ}
begin{split}
,text{Pr}(mathbf{Z}|mathbf{pi}) &= prod_{n = 1}^N ,text{Pr}(mathbf{z_n}|mathbf{pi}) \
&= prod_{n = 1}^N prod_{k = 1}^K pi_k^{z_{n, k}},
end{split}
end{equation}
and, similarly, combining all training images 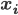
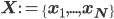
begin{equation} label{eq:probXgivZ}
begin{split}
,text{Pr}(mathbf{X}|mathbf{Z}, mathbf{mu}, mathbf{pi}) &= prod_{n = 1}^N ,text{Pr}(mathbf{x_n}|mathbf{z_n},mathbf{mu},mathbf{pi}) \
&= prod_{n = 1}^N prod_{k = 1}^K ,text{Pr}(mathbf{x_n} | mathbf{mu_k})^{z_{n, k}} \
&= prod_{n = 1}^N prod_{k = 1}^K left( prod_{i = 1}^D mu_{k, i}^{x_{n, i}} (1 – mu_{k, i})^{1 – x_{n, i}} right)^{z_{n, k}}.
end{split}
end{equation}
From the last two equations and the probability chain rule, the complete data likelihood can be written as:
begin{equation} label{eq:probXandZ}
begin{split}
,text{Pr}(mathbf{X}, mathbf{Z}| mathbf{mu}, mathbf{pi}) &= ,text{Pr}(mathbf{X} | mathbf{Z}, mathbf{mu}, mathbf{pi}) ,text{Pr}(mathbf{Z}| mathbf{mu}, mathbf{pi}) \
&= prod_{n = 1}^N prod_{k = 1}^K left( pi_k prod_{i = 1}^D mu_{k, i}^{x_{n, i}} (1 – mu_{k, i})^{1 – x_{n, i}} right)^{z_{n, k}},
end{split}
end{equation}
and thus the complete data log likelihood 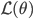
begin{equation}
begin{split}
mathcal{L}(theta) &= ln ,text{Pr}(mathbf{X}, mathbf{Z}| mathbf{mu}, mathbf{pi}) \
&= sum_{n = 1}^N sum_{k = 1}^K z_{n, k} left( ln pi_k + sum_{i = 1}^D x_{n, i} ln mu_{k, i} + (1 – x_{n, i}) ln (1 – mu_{k, i}) right).
end{split}
end{equation}
(Still following? Great. Take five, and below we will derive the E and M step update equations.)
2.2. E-M update equations for BMMs
In order to update the latent variable distribution (i.e. image assignment to clusters) at the expectation step, we need to set the probability distribution of 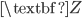
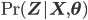
However, we cannot calculate this distribution exactly, hence we will have to approximate this assignment. A simple way of doing it is to replace the current values of 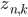
begin{equation} label{eq:z}
begin{split}
z_{n, k}^text{new} leftarrow mathbb{E}_{mathbf{Z} | mathbf{X}, mathbf{mu}, mathbf{pi}}[z_{n, k}] &= sum_{z_{n, k}} ,text{Pr}(z_{n,k} | mathbf{x_n}, mathbf{mu}, mathbf{pi}) , z_{n,k}\
&= frac{pi_k ,text{Pr}(mathbf{x_n} |mathbf{mu_k})}{sum_{m = 1}^K pi_m ,text{Pr}(mathbf{x_n} | mathbf{mu_m})} \
&= frac{pi_k prod_{i = 1}^D mu_{k, i}^{x_{n, i}} (1 – mu_{k, i})^{1 – x_{n, i}} }{sum_{m = 1}^K pi_m prod_{i = 1}^D mu_{m, i}^{x_{n, i}} (1 – mu_{m, i})^{1 – x_{n, i}}}.
end{split}
end{equation}
(Notice that after this update 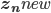
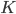
In the maximization step we need to maximize the model parameters (i.e. the mixing coefficients and the pixel distributions) using the update equation from earlier
Observe that
begin{align}
mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right] &= sum_{n = 1}^N sum_{k = 1}^K mathbb{E}_{mathbf{Z} | mathbf{X}, mathbf{mu}^text{old}, mathbf{pi}^text{old}} left[ z_{n, k} right] left( ln pi_k + sum_{i = 1}^D x_{n, i} ln mu_{k, i} + (1 – x_{n, i}) ln (1 – mu_{k, i}) right).
end{align}
The equation above can be maximized w.r.t. 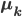
begin{align}
frac{partial}{partial mu_{m, j}} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right] &= sum_{n = 1}^N mathbb{E}_{mathbf{Z} | mathbf{X}, mathbf{mu}^text{old}, mathbf{pi}^text{old}} left[ z_{n, m} right] left( frac{x_{n, j}}{mu_{m, j}} – frac{1 – x_{n, j}}{1 – mu_{m, j}} right) \
&= sum_{n = 1}^N z_{n, m}^text{new} frac{x_{n, j} – mu_{m, j}}{mu_{m, j} (1 – mu_{m, j})} = 0 Leftrightarrow \
mu_{m, j} &= frac{1}{N_m} sum_{n = 1}^N x_{n, j} z_{n, m}^text{new},
end{align}
where 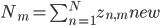
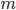
Then the full cluster 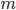
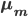
where 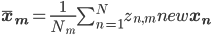
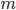
To maximize ![mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right]](http://blog.manfredas.com/wp-content/plugins/latex/cache/tex_2bdca63d7b1c6b52f12beb127b6707eb.gif)

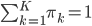
begin{equation*}
Lambda(theta, lambda) := mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right] + lambda left( sum_{k = 1}^K pi_k – 1 right).
end{equation*}
The optimizing solution can then be found again with simple partial derivatives:
begin{align}
frac{partial}{partial pi_{m}} Lambda(theta, lambda) &= frac{1}{pi_m} sum_{n = 1}^N z_{n,m}^text{new} + lambda = 0 Leftrightarrow \
pi_m &= -frac{N_m}{lambda},
end{align}
begin{align}
frac{partial}{partial lambda} Lambda(theta, lambda) &= sum_{k = 1}^K pi_k – 1 = 0 Leftrightarrow \
sum_{k = 1}^K pi_k &= 1.
end{align}
By combining these two results 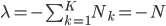
Done!
2.3. Summary
In summary, the update equations for Bernoulli Mixture Models using E-M are:
- Expectation step:
- Maximization step:
where
and
.
3. References
[Dempster et al, 1977] A. P. Dempster, N. M. Laird, D. B. Rubin. “Maximum Likelihood from Incomplete Data via the EM Algorithm”. Journal of the Royal Statistical Society. Series B (Methodological) 39 (1): 1–38.
[Bishop, 2006] C. M. Bishop. “Pattern Recognition and Machine Learning”. Springer, 2006. ISBN 9780387310732.

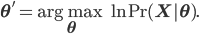
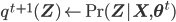
![mathbf{theta}^{t + 1} leftarrow underset{mathbf{theta}}{text{arg max }} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{t}} left[ mathcal{L}(theta) right]](http://blog.manfredas.com/wp-content/plugins/latex/cache/tex_ce39f6d35750f5ced3727687ba5d72c3.gif)
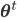
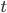
![mathbf{theta}^text{new} leftarrow underset{mathbf{theta}}{text{arg max }} mathbb{E}_{mathbf{Z} | mathbf{X}, theta^text{old}} left[ mathcal{L}(theta) right].](http://blog.manfredas.com/wp-content/plugins/latex/cache/tex_7b765729a0303627aca0d776d313549f.gif)