D3M: Improving Group Robustness via Dataset Selection
Machine learning models are increasingly making decisions in high-stakes
scenarios, from healthcare to finance to criminal justice. These models are
trained on large-scale datasets that often contain biased
data. As a result, these models often exhibit disparate performance
across different subgroups of the data. For instance, facial recognition systems
have been shown to perform poorly on images of Black women, while medical
imaging models struggle with X-rays of patients without chest drains. Such
biases can lead to serious real-world consequences when these models are used to
make decisions affecting different demographic groups.
The above issue motivates the problem of group
robustness, that is the task of minimizing
the worst-case loss over a predefined set of groups in the training data, where
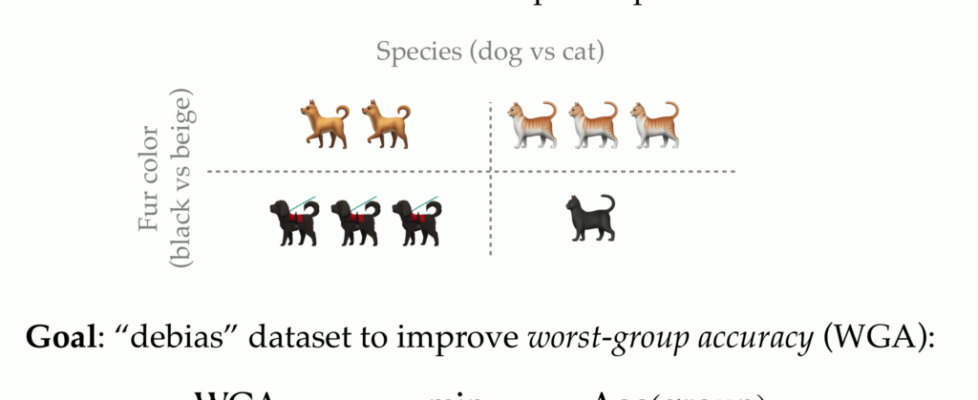
groups come from different sources. As a running example, consider the simple
classification task below—here, the inputs are images of animals, the labels are
“bird” or “horse,” and there is an additional feature (pose) that is spuriously
correlated with the label on the training set. The possible groups are thus
“bird + face”, “bird + full body”, “horse + face”, and “horse + full body”. The
goal of the group robustness problems is to minimize the worst-case loss over
groups. In other words, we want to maximize the worst-group accuracy (WGA).
How can we ensure that the model performs well in this regard?
A natural approach is to
change
the
learning
algorithm in a way that equalizes model
performance across groups. One such model intervention is Group
DRO which modifies the training procedure to
explicitly optimize for worst-group performance. Other approaches like
DFR retrain the last layer of the model on a
less biased dataset.
An alternative (and complementary) approach attempts to nullify the bias at its
source—the data. Rather than changing the learning algorithm, such data intervention
approaches aim to design datasets that naturally lead to “unbiased”
models (i.e., ones that have good WGA). For instance, dataset balancing involves
sampling an equal amount of data from each subgroup during training. This
approach has been shown to be surprisingly
effective compared to more complex (model)
interventions. However, dataset balancing (a) requires group information for the
entire training set, which can often be prohibitively expensive to obtain(b)
removes a large part of the training data when the training set is highly
imbalanced, leading to decreased performance.
More broadly, dataset balancing is a very coarse way to intervene on the
dataset. In particular, it makes the (strong) assumption that all examples
within a group impact the model’s group robustness equally.
In our latest work, we develop a new approach for designing datasets
that induce group robustness. This approach revolves around understanding how
individual data points drive a model’s biases. And if you’ve followed our blog
posts for the past year, you know where this is going: we’re going to leverage
TRAK to specifically optimize our datasets
for worst group accuracy!
Optimizing datasets for group robustness
Recall that our objective here is to maximize worst-group accuracy on some held
out dataset, given control over the membership of the training data. So,
formally, given a learning algorithm A and a dataset S, we would like to solve
the optimization problem:
[max_{D subseteq S} WGA(text{running } A text{ on } D).]
How can we do that? Clearly, the search space of possible subsets D is
combinatorial, so we can’t hope to apply brute force approaches. Instead, we
need to understand how the dataset D changes WGA on the held out set.
Recently, we have been working on writing model predictions in terms of the
training data in our work on
datamodels and
TRAK. There, the setup was as follows:
there is a model (e.g., a neural network) $theta(S)$ resulting from training on
a dataset $S$, and $f(z, theta(S))$ is that model’s output of interest on an
example $z$ (e.g., the loss on $z$). We then found, in short, a linear function
$h_z(D)=sum_{iin D} beta^{(z)}_i$ that approximates $f(z, theta(D))$
for any given subset $D$ of $S$. In particular, we demonstrated that the
function $h_z$ can (efficiently) answer the question “what would the
prediction of $theta$ be on $z$, had we trained $theta$ on $D$ instead of
$S$?”.
A simplified objective
With the above approximation for deep networks in hand, we can plug it into our
dataset optimization problem in order to maximize WGA! Doing so, we end up with
the following objective:
[max_D, min_Gleft{ text{ predicted WGA according to } h(D) right}]
This problem is still “combinatorial” in flavor (as we still are optimizing over
discrete subsets of the dataset) but if we replace WGA, the optimization target,
with a “smoother” proxy—namely, worst-group loss For
technical reasons, it turns out that using correct-class margin i.e.,
$log(p/1-p)$, instead of the cross entropy loss $-log(p)$ leads to better empirical
results. , we are now dealing with a linear objective. In
particular, we have
[max_D, min_G left{ sum_{z in text{held out set}} h_z(D) right} =
max_D, min_G left{ sum_{z in text{held out set},, iin D} beta^{(z)}_i right}]
This is now a much easier optimization problem to tackle!
Aside: Some recent work from our lab has applied a similar approach—optimizing
model performance using datamodel-predicted outputs in place of real outputs—to
select pre-training data for language models. Check it
out!
D3M: Data Debiasing with Datamodels
To solve (1), we approximate the inner minimization above using the smooth
minimum function—turning our optimization problem into a trivial linear
minimization [1]
Note that if we had perfect datamodels $beta$, we could have expressed equation
1 as a linear program and solved directly; empirically, however, we found this
approach to be unstable and highly sensitive to the estimated coefficients
$beta$.. More
specifically, we employ the following procedure:
- Partition the held out set $S_{test}$ into ${S_1, S_2,…S_{vert Gvert}}$ based on group attributes $gin G$, and let $ell_g$ be the average loss on $S_g$.
- For each set of samples from a group $g$, we compute the average predicted loss on that group $tau(g) := frac{1}{vert S_gvert} sum_{zin S_g} h_z(S)$.
- For each training example $z_i$, define a group alignment score $T_i$ as:
[T_i = exp(ell_g) * tau(g)_i.]
Intuitively, the group alignment score captures the weighted average (over groups) of the example’s contribution to each group loss, upweighting groups for which the loss is high.
- Remove the training examples with the most negative group alignment scores from the training set.
At a high level, training examples with high group alignment scores disproportionately drive the increase in loss on underperforming groups.
Results
We apply our method on standard group robustness benchmarks, and observe consistent gains over the existent state of the art methods:
Taking a closer look, we compare our approach (in green, below) to a
model-agnostic approach that indiscriminately removes samples from the majority
groups (in orange, below) as we vary the number of removed examples. (Note that
the latter approach exactly coincides with dataset balancing, when the number of
removed examples is high enough–we visualize this using the dashed black line
below):
We find that our approach is able to pinpoint relatively few examples that
contribute most negatively to worst-group accuracy, and thus outperform dataset
balancing while removing vastly fewer examples, and without requiring group
labels for the training set!
Overall, D3M highlights the utility of a model-aware yet data-centric
perspective on model behavior!