The N-Queen Problem: A Simple Way to Understand Backtracking
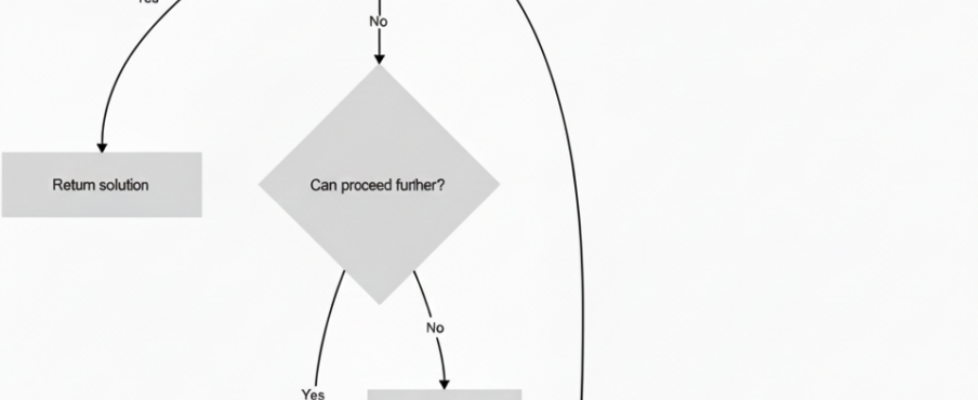
Backtracking is a problem-solving technique that helps us explore different possibilities in a structured way. The idea is simple — move forward by making a choice, and if that choice does not lead to a valid solution, go back, undo the last step, and try a different path. In this article, we will understand this approach step by step and later see how it is applied through the N-Queen problem.
Backtracking if you just split the words its back and tracking. According to basic English meaning it just mean to track back the path which you took and here in the tech world it abide to the same meaning i.e., just retrieve back the last operation you did and just undo it.
It is a type of Brute — force search.
It is a algorithmic method of solving the problem by exploring all the possible solution. In this the solution is examined at each step to check if it still passes the condition and if it doesn’t meet the criteria the algorithm holds back from the previous step and tries another solution.
To understand how backtracking works in practice, it is important to focus on the sequence of steps involved rather than the final answer. Backtracking follows a simple pattern: choose an option, explore it fully, and if it fails, undo the choice and try another one. This process continues until a valid solution is found or all possibilities are exhausted.
It is kind of hit and trial approach.
If you deep dive into how backtracking works its just simple approach:-
- you just choose one choice which might take you to the solution.
- you then just explore with the choice you made.
- While exploring you check the validity of the choice, if its leading to the correct solution then you can reach to the solution and if not then just undo it.
- you keep repeating it until you found your solution.

While backtracking provides a clear and systematic way to explore all possible solutions, it is not always the most efficient approach. Like every algorithmic technique, backtracking comes with its own strengths and limitations. Let’s now look at the advantages and disadvantages of using backtracking.
Advantages:
- It guarantees finding a solution.
- It is flexible.
- It is easy to understand.
Disadvantages:
- The time complexity is High.
- Its implementation is different.
- It follows brute force Approach which make it inefficient in some cases.
Understanding the advantages and disadvantages of backtracking helps us decide where this approach is most effective. Backtracking is widely used in problems where multiple choices exist and all possible solutions need to be explored. Let’s now look at some common applications of backtracking.
Application:
- N-queen problem
- Sum of subset problem
- Graph coloring
- Hamiltonian Cycle
Among all the applications of backtracking, the N-Queen problem is one of the most popular and easy-to-visualize examples. It clearly demonstrates how backtracking explores choices, checks constraints, and undoes decisions when a path fails. Let’s now understand the N-Queen problem and see how backtracking is applied to solve it.
N-Queen Problem
In this there is N*N size chess board and on which we have to place the N queens so they don’t attack each other.
Before getting exactly to N -Queen, Let’s take some more realistic example so you can understand it better.
Sudoku, we all must have played it. do you remember how we used to solve it, if not then its just have the 9*9 square box further divided in 3*3 square box and you have to fill the numbers to the place which is empty but the condition is number shouldn’t be repeated vertically, horizontally, and inside the 3*3 box and while solving it you just sometimes do hit and trial and just try different number if its not taking us to the correct solution.
Now before going to our problem, you must all be knowing how the queen moves in chess, its horizontally, vertically and diagonally.
For simple understanding we are taking our chess board is of size 4*4.
So, just combine the scenario of sudoku and chess i.e., we have to place the queen so they don’t attack each other so one queen should not be in the horizontal range, vertical range and diagonal range of the another queen.
We have 4*4 chess board and 4 queens i.e., q1, q2, q3, q4.

Now Let’s place the First Queen q1 in the (1,1) cell and eliminate the position for the other queens where they can’t be placed.

Alright, let’s place the Second Queen q2 in the (2,3) cell and eliminate the position for the other queens where they can’t be placed.

let’s place the Third Queen q3 in the only cell that’s left.

As you noticed, the fourth queen was left to be placed. so we will just back track the queen q2 and q3. Placing the q2 and q3 in different location.

As you noticed, the fourth queen was again left to be placed. so we will just back track the queen q1, q2 and q3. Placing all the queen in different locations.

Solution: [q1(1,2) , q2(2,4) , q3(3,1) , q4(4,3)]
We were able to solve the problem of placing the all the queen in the chess board by backtracking. For better understanding try for the 8*8, so that you get the clear idea how it is happening.
For 8*8,
Solution: [q1(1,6), q2(2,4), q3(3,7), q4(4,1), q5(5,8), q6(6,2), q7(7,5), q8(8,3)]
Through the N-Queen problem, we can clearly see how backtracking works in practice. When a queen is placed in a position that prevents further placements, the algorithm does not stop. Instead, it backtracks by removing the last placed queen and tries a different position. This process continues until a valid arrangement is found, proving that backtracking is not about guessing blindly, but about systematically exploring all possible solutions.
Backtracking is a powerful problem-solving technique that teaches us how to approach complex problems in a structured way. The N-Queen problem serves as a perfect example to understand this approach, showing how incorrect decisions are reversed and corrected step by step. Rather than focusing on memorizing solutions, understanding the idea of backtracking helps in solving a wide range of problems more effectively. With practice, this way of thinking becomes intuitive and can be applied to many real-world and algorithmic challenges.
The N-Queen Problem: A Simple Way to Understand Backtracking was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.